These puzzles have to do with a strange island inhabited by two types of people: people who only tell the truth (knights) and people who only tell lies (knaves). Raymond Smullyan collected dozens of puzzles like this in his book, What is the Name of This Book?. The following list progresses quickly from easy to very difficult. When you have mastered these, try the Hardest Logic Puzzle Ever.
1. Two people, Red and Blue, stand before you. Red says, “We are both knaves.” What are they really?
See Answer
2. Two people again. Red says, “We are both the same type of people,” and Blue says, “We are each different types of people.” What are their identities?
3. You come to a fork in a road and need to learn which path leads to your destination. Two individuals are standing there. You know that one is a knight and one is a knave, but you don’t know which is which. What single yes-or-no question could you ask of one of the islanders to learn the correct path?
See Answer
4. Now you encounter a fork in the road but there is only one inhabitant standing there, and you do not know whether he is a knight or a knave. What one yes-or-no question could you ask to learn the correct path?
See AnswerFirst of all, suppose that the person is a knight and the path is correct. The knight answers yes. If the person is a knight and the path is not correct, then the knight will answer no. If the person is a knave and the path is correct, then the knave would lie and say no if asked. However, you are asking if he would say yes if asked, so he must lie and say yes. If the person is a knave and the path is incorrect, then the knave would lie and say yes if asked. But you are asking if he would say yes if asked, so he must lie and say no.
5. To complicate matters, a new island is discovered, with a third type of inhabitant: spies, who can either tell the truth or lie. You encounter three people, one of each, but you don’t know which is which. Red says, “I am a knight.” Blue says, “Red is telling the truth.” Green says, “I am the spy.” Who is what?
6. Now add the wrinkle of language difficulties. On yet another island, the inhabitants are all either knights or knaves, and though they understand English, they will not utter the words Yes and No. They use “Ja” and “Da,” but we do not know which means Yes and which means No. Upon encountering an inhabitant of this island, you ask, “Does Ja mean Yes?” He answers, “Ja.” Have you learned what Ja means? Have you learned whether the person is a knight or a knave?
See Answer
7. You encounter another inhabitant of the same island and are determined to discover the meanings of Ja and Da. What one yes-or-no question can you ask in order to learn this?
See Answer
8. Suppose that you have not determined the meanings of Ja and Da, but you encounter one inhabitant of the same island at a fork in the road and you must find out the correct path to take. Can you do it with one yes-or-no question?
See AnswerIf the person is a knight and it is the correct path and Ja means Yes, then he will answer Ja. If the person is a knight and it is the correct path and Ja means No, then he will answer Ja (No I would not answer no).
If the person is a knight and it is the wrong path and Ja means yes, then he will answer Da (no). If the person is a knight and it is the wrong path and Ja means no, then he will answer Da (yes I would say no).
If the person is a knave and it is the correct path and Ja means yes, then he will lie and answer Ja (yes I would say yes). If the person is a knave and it is the correct path and Ja means no, then he will lie and answer Ja (no I would not say no).
If the person is a knave and it is the wrong path and Ja means yes, then he will lie and answer Da (no I would not say yes). If the person is a knave and it is the wrong path and Ja means no, then he will lie and answer Da (yes I would say no).
Your solution to #4 gives you no information and you are as you were when you arrived. Asking that question will not resolve your dilemma.
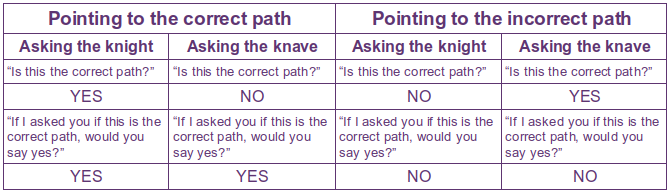
The new information comes from an added layer of abstraction with regard to the knave. To understand #4, suppose you are the knave, so you must always lie. A traveler approaches, who does not know whether you are a knight or a knave. If he points to a path, and simply asks, “Is this the correct path?” then you must lie, so if it is the correct path, you say No and if it is not the correct path, you say Yes. This does not help the traveler. But if the traveler instead asks, “If I asked you if this is the correct path, would you say yes?” then your answer must change! If it is the correct path and you were asked if it is the correct path, you would lie and say No, so in answer to the question of whether you would say Yes, you must lie and say Yes. Similarly, if it was the incorrect path, your answer to the question, “Is this the correct path?” would be Yes (a lie), but your answer to the question, “If I asked you if this is the correct path, would you say yes?” must be No (a lie). This forces the knave into a double lie, revealing the correct path. The knight, on the other hand, would be telling the truth in answer to either question, so no new information is needed in that case. Here’s a chart to illustrate the difference between the two questions:
But I don’t think you know which path is correct.
A knight and a knave can both give yes no answers… so it depends whether the path is correct or not, which you still do not know…?
Sorry, no. The point is that you need to ask 2 questions to solve #4
Referring to the chart above, simply asking, “If I asked you if this is the correct path, would you say yes?” has the result that a Yes answer means it’s the correct path and a No answer means it’s the incorrect path, so you get the information you are seeking. Ironically, you would never find out whether you were talking to a knight or a knave. In a sense, “If I asked you if this is the correct path, would you say yes?” is a trick question, because it provides us with an extra layer of information, allowing us to get the information we seek with only one question.
for question 4 i would ask either one “if i asked your counterpart which path is correct what would they saw?” either answer would end up being a lie so take the opposite
Your solution to #3 fails.
Let’s have a look! A chart may be helpful in understanding #3 as well. Here again, the added layer of abstraction gives additional information, though here it is the knight’s answer that changes.
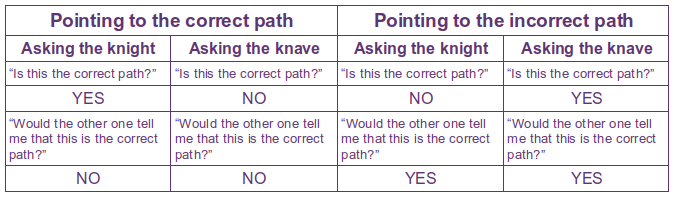
Would the solution for #4 also work for #3? I’ve gone through it and it seems it would.